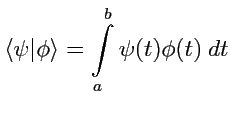1. Основные сведения из векторной алгебры
 1.3. Скалярное произведение векторов
1.3. Скалярное произведение векторов 
Углом между векторами

и

называется угол между равными им векторами,
имеющими общее начало. Он обозначается как
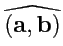
, (
рис.5)
Рис.5 К определению скалярного произведения векторов
Угол между векторами может принимать значения от
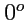
(для параллельных векторов) до
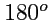
(для антипараллельных). Если
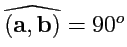
, то эти векторы называются
ортогональными, что обозначается как:
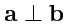
. Так как нулевой вектор
имеет произвольное направление, то угол между ним и ненулевым вектором, а также угол между
двумя нулевыми векторами может принимать любые значения из интервала
![$ [0^o,180^o]$](img51.png)
.
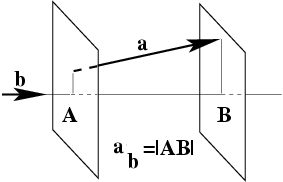
Проекцией вектора
 на направление вектора
на направление вектора

называется скаляр, обозначаемый
как
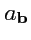
и равный длине отрезка, отсекаемого на прямой, проходящей через вектор

,
перпендикулярными к ней плоскостями, проведенными через концы векторов

и

, взятый
со знаком (+), если направление от проекции начала вектора

к проекции конца совпадает
с направлением вектора

, и со знаком (-) - в противном случае (
рис. 6).
Ясно, что
Рис. 6 Проекция вектора
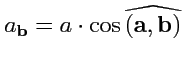 и
и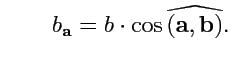
Скалярным произведением векторов

и

называется
скаляр, обозначаемый
как
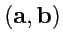
, или
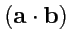
(это обозначение удобнее использовать, если выражение содержит
другие операции с векторами) или просто
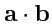
и равный
произведению модулей этих векторов на косинус угла между ними:
Очевидно, что
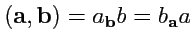
. Если
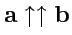
, то
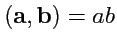
, в частности
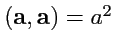
. Если
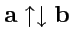
,
то
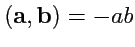
. Наконец, для
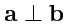
,
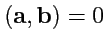
и соответственно
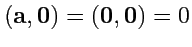
.
Из вышеприведенного определения скалярного произведения векторов как направленных отрезков
следуют свойства:
1.
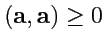
, причем
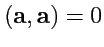
, если
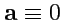
;
2.
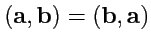 (коммутативность);
(коммутативность);
3.
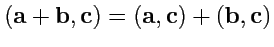 (дистрибутивность);
(дистрибутивность);
4.
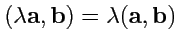 ;
;
Если в линейном пространстве задано скалярное произведение векторов, т. е. правило сопоставления
двум любым векторам - числа, удовлетворяющее свойствам (1-4), то такое пространство называется
евклидовым.
Подчеркнем еще раз: скалярное произведение даже на одном линейном пространстве можно задавать
по-разному, но оно обязательно должно удовлетворять перечисленным свойствам (1-4). В качестве
примера иных, чем рассмотренное, скалярных произведений, можно указать следующеe (для обозначения
таких типов произведений часто используют угловые скобки):
в упоминавшемся выше линейном пространстве функций. Легко проверить, что (1-4) выполняются,
как следствие свойств определенных интегралов.

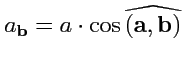 и
и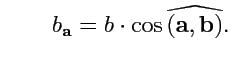
![]() (коммутативность);
(коммутативность);
![]() (дистрибутивность);
(дистрибутивность);
![]() ;
;