1. Основные сведения из векторной алгебры
 1.2. Определение вектора и линейные операции над векторами
1.2. Определение вектора и линейные операции над векторами 
Под вектором в элементарной математике понимают направленный отрезок. Этот отрезок
изображается стрелкой и обозначается или одной буквой со стрелкой (
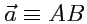 )
(рис.1.1),
)
(рис.1.1),
Рис.1. Векторы
либо, как мы условимся в настоящем издании, жирным шрифтом
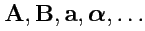
.
Модулем (абсолютной величиной) вектора называется длина отрезка, изображающего этот вектор.
Модуль обозначается
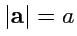 . Модуль вектора является скаляром. Если начало и конец вектора
совпадают, то вектор называется нулевым и обозначается как
. Модуль вектора является скаляром. Если начало и конец вектора
совпадают, то вектор называется нулевым и обозначается как
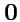 . Если модуль вектора
равен нулю, а направление не определено, то можно считать, что он направлен в любую сторону.
. Если модуль вектора
равен нулю, а направление не определено, то можно считать, что он направлен в любую сторону.
Коллинеарными называются два ненулевых вектора, лежащих на одной прямой, либо на
параллельных прямых. Коллинеарные векторы
 и
и
 будем обозначать
как
будем обозначать
как
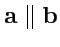 . Если неколлинеарные векторы направлены одинаково, их называют
параллельными (сонаправленными) -
. Если неколлинеарные векторы направлены одинаково, их называют
параллельными (сонаправленными) -
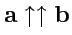 ; противоположно направленные
коллинеарные векторы называют антипараллельными
; противоположно направленные
коллинеарные векторы называют антипараллельными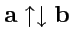
Два или более векторов называются компланарными, если они лежат в одной плоскости. Очевидно, что два коллинеарных вектора всегда компланарны.
Будем считать, что вектор не зависит от того, где находится начало (такие вектора называются
свободными). Два свободных вектора называются равными, если они параллельны и имеют
равные модули:
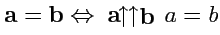 .
.
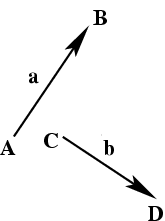
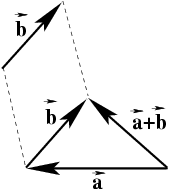
Пусть имеется два ненулевых вектора

и

(
рис.2). Из конца вектора

отложим вектор, равный

. Тогда
суммой векторов

и

называется вектор, соединяющий начало вектора

и конец вектора

(
правило треугольника).
Рис.1.2 Сложение векторов
Можно также
использовать следующее из
правила треугольника
правило параллелограмма: суммой двух неколлинеарных векторов

и

называется вектор, идущий из общего начала векторов по диагонали
параллелограмма, построенного на этих векторах (
рис.3). Оба правила применимы как
для коллинеарных векторов, так и в случае, когда один или два вектора являются нулевыми.
Рис.3. Сложение векторов
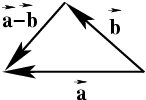
Вектор, антипараллельный данному вектору

и имеющий такой же модуль, называется
противоположным вектору

и обозначается
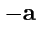
. Очевидно, что сумма
противоположных векторов является нулевым вектором:
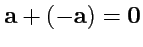
. Разностью
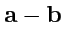
векторов

и

называется сумма вектора

и вектора,
противоположного вектору

:
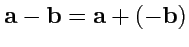
. Соединим начала векторов

и
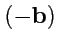
, тогда вектор
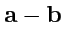
направлен из конца вектора

в конец
вектора

(рис.
4).
Рис.4. Разность векторов
Произведением вектора

на число
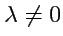
называется вектор

с модулем
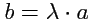
, причем
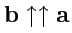
при
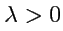
и
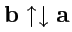
при
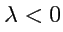
. Геометрически умножение
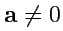
на
число
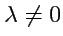
означает "растяжение" вектора

в
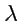
раз с сохранением
направления при
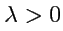
и изменением на противоположное при
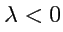
.
Из приведенных выше правил сложения векторов и умножения их на число следуют очевидные
утверждения:
1.
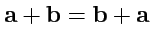 (сложение коммутативно);
(сложение коммутативно);
2.
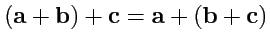 (сложение ассоциативно);
(сложение ассоциативно);
3.
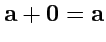 (существование нулевого вектора);
(существование нулевого вектора);
4.
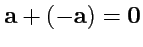 (существование противоположного вектора);
(существование противоположного вектора);
5.
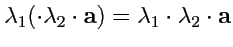 (сложение
ассоциативно);
(сложение
ассоциативно);
6.
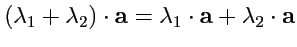 (умножение
на число дистрибутивно);
(умножение
на число дистрибутивно);
7.
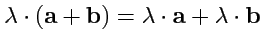 (сложение векторов
дистрибутивно);
(сложение векторов
дистрибутивно);
8.
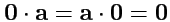 .
.
В линейной алгебре множество элементов произвольной природы, на котором определены операции сложения
и умножения на число, а также справедливы утверждения (
1-8), называют
линейным пространством,
а сами элементы - векторами (в широком смысле) этого пространства. Таким образом, введенные векторы,
как направленные отрезки, образуют линейное пространство.
В физике часто приходится иметь дело с такими свойствами, для определения которых, кроме их
численного значения, необходимо указывать и направление в пространстве. Например, скорость,
ускорение, сила, момент силы, напряженность электрического или магнитного поля и т. п. Из
физического определения этих величин следует, что они являются векторами в своем линейном
пространстве - для них выполняются (
1-8). Эти физические величины имеют такую же "внутреннюю
структуру", что и направленные отрезки. Поэтому логически непротиворечивые правила работы
с такими физическими характеристиками можно изучать на примере "работы" с математическими
векторами из линейного пространства. Подчеркнем, что свойства (
1-8) являются определяющими
для вектора. Например, поворот твердого тела на конечный угол вокруг некоторой оси можно
задавать с помощью направленного отрезка
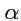
, параллельного оси вращения и по
модулю равного углу поворота. Но такой "поворот"
не будет вектором, так как повороты
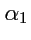
и
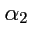
вокруг разных осей, вообще говоря, не коммутруют:
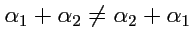
и, таким образом, свойство 1 из (
1-8) не выполняется.
В противоположность конечным поворотам, повороты на бесконечно малые углы являются векторами.
С другой стороны, конкретные функции из множества функций
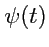
с одной областью определения,
например,
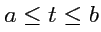
, нельзя представить постредством направленных отрезков, но для них,
тем не менее, справедливы все свойства линейного пространства, поэтому функции можно считать
векторами в широком смысле.

![]() (сложение коммутативно);
(сложение коммутативно); ![]() (сложение ассоциативно);
(сложение ассоциативно); ![]() (существование нулевого вектора);
(существование нулевого вектора); ![]() (существование противоположного вектора);
(существование противоположного вектора); ![]() (сложение
ассоциативно);
(сложение
ассоциативно); ![]() (умножение
на число дистрибутивно);
(умножение
на число дистрибутивно); ![]() (сложение векторов
дистрибутивно);
(сложение векторов
дистрибутивно); ![]() .
.