1. Основные сведения из векторной алгебры
 1.9. Координатное представление векторов.
1.9. Координатное представление векторов. 
Ранее было показано, что если задан определенный, например, декартовый базис
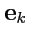
, то
любой вектор

представим в виде линейной комбинации базисных векторов:
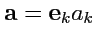
. Но так как базис
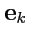
фиксирован, то различные векторы будут
различаться своими координатами
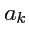
, т. е. тройка координат полностью определяет вектор в
заданном базисе. Покажем, что и любые операции с векторами задаются действиями над координатами
векторов.
1. При сложении векторов координаты складываются:
Действительно,
Так как векторы базиса
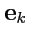
являются линейно независимыми, то из равенства нулю последней линейной комбинации следует, что
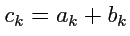
.
2. При умножении вектора на скаляр координаты вектора умножаются на скаляр:
Отметим, что для операции 1 и 2 выполняются все законы (
1)-(
11), определяющие
линейное пространство, поэтому множество троек чисел, для которых определены операции 1 и 2,
образуют линейное пространство, а сами тройки являются векторами этого пространства. Хотя
направленные отрезки и тройки чисел - это различные геометрические объекты, между ними существуют
определенные соответствия (через базисные векторы).
3. Скалярное произведение двух векторов равно сумме попарных произведений их координат
где было использовано свойство (
13).
4. Модуль вектора равен положительному корню из суммы квадратов координат:
в частности, для радиус-вектора
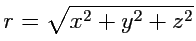
. Доказательство вытекает из 3, если
положить
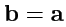
.
5. Векторное произведение.
Согласно (
15) векторное произведение базисных ортов можно выразить с помощью
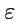
-символа и тогда, если
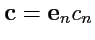
, то
а вектор
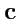
запишется как
В явной форме для
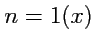
, получим
и аналогично для других координат векторного произведения. Легко проверить, что полученные выражения
для координат векторного произведения можно получить раскрывая определитель:
6. Смешанное произведение векторов
Представление смешанного произведения векторов через их координаты, записанное выше,
доказывается аналогично рассмотренным ранее.
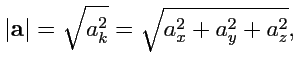
![\begin{displaymath}[{\mathbf a},{\mathbf b}]=
\left\vert
\begin{array}{ccc}
{\m...
... & a_z \\ [0.5em]
b_x & b_y & b_z \\
\end{array}\right\vert.
\end{displaymath}](img249.png)
![\begin{displaymath}
({\mathbf a},[{\mathbf b},{\mathbf c}]) = \varepsilon_{ijk}a...
... & b_z \\ [0.5em]
c_x & c_y & c_z \\
\end{array}\right\vert.
\end{displaymath}](img250.png)