1. Основные сведения из векторной алгебры
 1.10. Преобразование ортов декартовых базисов
1.10. Преобразование ортов декартовых базисов 
Как уже отмечалось выше, в линейном пространстве можно выбрать сколь угодно много базисов.
Наиболее удобный для работы с векторами - это декартов базис, но и он определяется
неоднозначно. В случае работы со свободными векторами, их можно привести к общему началу.
Но и в этом случае можно выбрать сколь угодно много ортонормированных троек векторов,
развернутых одна относительно другой.
Пусть даны два декартовых базиса

и
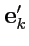
. Найдем связь
между ортами этих базисов. Для этого разложим орты базиса
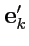
по базису

и наоборот:
 |
(20) |
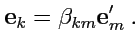 |
(21) |
Коэффициенты разложения перенумерованы с помощью двух индексов, один из которых свободный
(
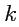
), второй - индекс суммирования (
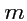
). Равенство (
20) называется
прямым преобразованием ортов, а (
21) -
обратным. Если подставить
(
21) в (
20), соответственно заменяя индекс суммирования, то можно
получить:
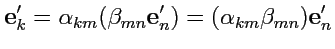 |
(22) |
и, сравнивая коэффициенты прsи одинаковых ортах в левой и правой частях (
22),
приходим к выводу:
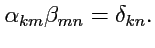 |
(23) |
Так связаны между собой коэффициенты прямого и обратного преобразований ортов. Далее, умножим
скалярно обе части (
20) на вектор
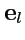
, а (
21) - на
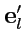
.
Тогда
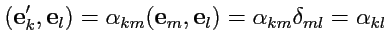 |
(24) |
 |
(25) |
Заменим индексы
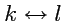
, тогда:
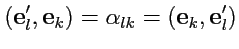 |
(26) |
и, сравнивая с (
25), получим связь между коэффициентами прямого и обратного
преобразований декартовых ортов:
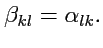 |
(27) |
Используя (
24), соотношения (
20) и (
21), можно переписать в виде:
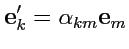 |
(28) |
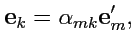 |
(29) |
а соотношение (
23) в виде
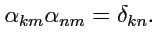 |
(30) |
Соотношения (
28) и (
29) определяют так называемое
линейное
ортогональное преобразование декартового базиса, а коэффициенты этого преобразования
образуют ортогональную матрицу, определяемую условием (
30). В матричной форме,
т. е. с использованием правила умножения "строка на столбец" это соотношение можно переписать
в виде:
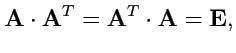 |
(31) |
где
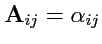
- матрица ортогонального преобразования,
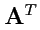
-
транспонированная матрица,
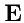
- единичная матрица:
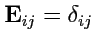
.
Из (
30) следует, что сумма квадратов матричных элементов для любой строки
матрицы ортогонального преобразования равна единице, а сумма попарных произведений
матричных элементов двух разных строк равна нулю. Легко показать, что аналогичные
соотношения выполняются и для столбцов матрицы ортогонального преобразования.
Используя (
24), можно записать матрицу ортогонального преобразования декартовых
ортов в явном виде:
 |
(32) |
где
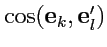
- косинус угла между соответствующими ортами двух декартовых
базисов.
Так как
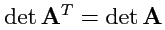
, а
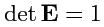
, то из (
30) следует, что
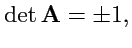 |
(33) |
т. е. определитель матрицы ортогонального преобразования может быть равен только плюс или
минус единице.
Ортогональные преобразования, для которых
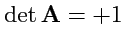
, называются ортогональными
преобразованиями
первого рода. Можно показать, что всем поворотам систем координат
соответствуют преобразования первого рода. Иными словами, два декартовых базиса, связанных
друг с другом ортогональным преобразованием первого рода, получаются один из другого
путем непрерывного поворота всех ортов одновременно.
Ортогональные преобразования, для которых
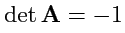
, называются ортогональными
преобразованиями
второго рода. Примером такого преобразованя может служить инверсия
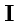
, которая меняет направления всех векторов на противоположные, а правый декартов
базис переводит в левый и наоборот. Перейти от правого базиса к левому с помощью непрерывного
поворота невозможно. Матрица преобразования инверсии равна:
![$\displaystyle {\mathbf I} = \left(\hspace{-0.3em} \begin{array}{rrr} -1 & 0 & 0 \\ [0.5em] 0 & -1 & 0 \\ [0.5em] 0 & 0 & -1 \\ \end{array} \right)$](img280.png) |
(34) |
и в сокращенной записи
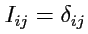
. Можно также показать, что любое преобразование
второго рода представимо как последовательное действие (произведение) инверсии и преобразования
первого рода. Поэтому преобразование второго рода, как уже отмечено ниже, переводит правый базис
в левый.