5. Основы тензорного анализа

Признак тензорности величины 5.8. Псевдотензоры Единичный псевдотензор Леви-Чивиты

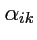
Ранее было показано, что все линейные ортогональные преобразования в зависимости от знака определителя матрицы $ \alpha_{ik}$, можно разделить на собственные и несобственные. Закон изменения компонент тензоров может зависеть от типа преобразования и по этой причине различают:
  1. истинные (полярные) тензоры, компоненты которых преобразуются "обычным" способом

  1. $\displaystyle T'_{ik...}=\alpha_{im}\alpha_{kn}T_{mn...} $

    при любых типах преобразований;
  2. псевдотензоры (аксиальные), которые преобразуются по правилу
    $\displaystyle \Pi'_{ik...}=\Delta\alpha_{im}\alpha_{kn}\Pi_{mn...} $

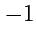
Как следует из определения, при собственном преобразовании отличить тензор от псевдотензора нельзя, а при несобственном - это сделать можно за счет появления дополнительного множителя, равного $ -1$.
Векторный анализ в криволинейных координатах Литература
Признак тензорности величины   Содержание   Единичный псевдотензор Леви-Чивиты