5. Основы тензорного анализа
 5.7. Признак тензорности величины
5.7. Признак тензорности величины 
Если величина
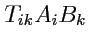
является скаляром, а
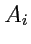
и
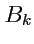
- компоненты векторов, то
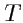
является тензором второго ранга.
Доказательство: так как
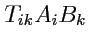
- скаляр, то в другой системе координат его значение не
меняется
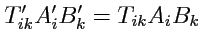
, но поскольку
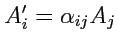
и
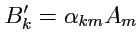
, то
и отсюда, в силу независимости набора величин
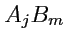
, получаем, что
т. е. закон преобразования компонент тензора второго ранга.