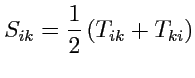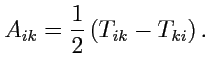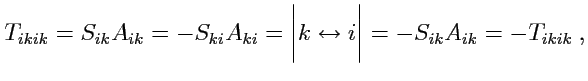5. Основы тензорного анализа

Тензорная алгебра 5.6. Симметричные и антисимметричные тензоры Признак тензорности величины

Тензор ранга $ n$ называется симметричным или антисимметричным по каким-либо индексам, если имеет место следующее соотношение:
$\displaystyle A_{...i...k...} = \pm A_{...k...i...}\ ,$ (279)
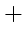
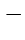
где знак "$ +$" в (279) отвечает симметричному, а "$ -$" антисимметричному тензору.

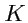
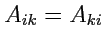
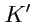
Свойство: симметрия тензоров не зависит от выбора координатной системы. Действительно пусть в системе $ K$ задан симметричный тензор 2-го ранга, т. е. $ A_{ik}=A_{ki}$. Тогда, переходя в систему $ K'$,получим
$\displaystyle A'_{lm}=\alpha_{li}\alpha_{mk}A_{ik} = \alpha_{li}\alpha_{mk}A_{ki} = \alpha_{mk}\alpha_{li}A_{ki} = A'_{ml}. $

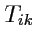
      Пример 5-1. Рассмотрим произвольный тензор ранга 2 - $ T_{ik}$ и построим симметричный тензор с компонентами
$\displaystyle S_{ik} = \frac{1}{2}\left( T_{ik}+T_{ki} \right) $
и, поступая аналогично, антисимметричный тензор
$\displaystyle A_{ik} = \frac{1}{2}\left( T_{ik}-T_{ki} \right). $
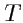
Тогда, очевидно, что тензор $ T$ 2-го ранга может быть представлен в виде суммы симметричного и антисимметричного тензоров как
$\displaystyle T_{ik} = S_{ik} + A_{ik}. $
Для тензоров высших рангов возможно аналогичное построение, при этом, однако, будет получаться большее число новых тензоров, которые не обязательно будут полностью симметричными или антисимметричными.

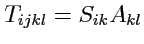
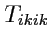
      Пример 5-2. Свертка тензорного выражения по паре "симметричных" и "антисимметричных индексов" дает ноль. Действительно, рассмотрим тензор 4-го ранга, построенный из симметричного и антисимметричного тензоров как $ T_{ijkl}=S_{ik}A_{kl}$ и вычислим его свертку $ T_{ikik}$, тогда
$\displaystyle T_{ikik}=S_{ik}A_{ik} = -S_{ki}A_{ki} = \biggl\vert k\leftrightarrow i \biggr\vert = -S_{ik}A_{ik}= -T_{ikik}\ , $
откуда следует, что $ T_{ikik}=0$.
Векторный анализ в криволинейных координатах Литература
Тензорная алгебра   Содержание   Признак тензорности величины