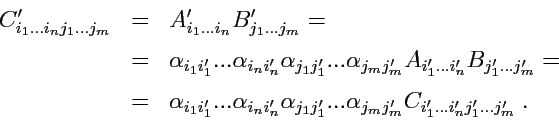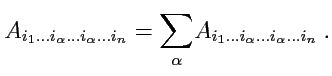5. Основы тензорного анализа
 5.5.1. Тензорная алгебра. Сложение тензоров.
5.5.1. Тензорная алгебра. Сложение тензоров. 
Пусть заданы тензоры
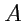
и
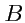
одинакового ранга, тогда величина
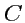
, построенная по
правилу
называется суммой тензоров
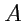
и
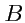
и является также тензором ранга

. Для доказательства второго утверждения вычислим значения
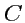
в системе
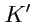
. Тогдa
 5.5.2. Тензорная алгебра. Умножение тензоров.
5.5.2. Тензорная алгебра. Умножение тензоров. 
Пусть даны два тензора
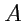
(ранга

) и
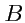
(ранга
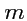
). Тогда, величина
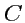
, образованная из компонент тензоров
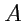
и
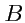
, по правилу
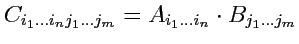 |
(275) |
называется
произведением тензоров
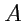
и
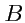
и является тензором ранга
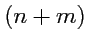
. Вычислим
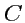
в системе
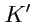
. Тогда
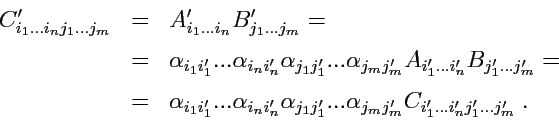 |
(276) |
 5.5.3. Тензорная алгебра. Свертка тензоров.
5.5.3. Тензорная алгебра. Свертка тензоров. 
Пусть задан тензор
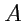
ранга

с компонентами
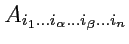
.
Сверткой тензора
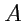
называется суммирование компонент по каким-либо парам индексов
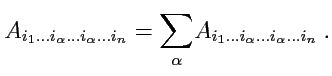 |
(277) |
Выполняя сверки по различным парам индексов, можно получать новые тензоры, ранг которых
будет уменьшаться на 2 единицы от "сворачивания" каждой пары индексов. Для примера рассмотрим
свертку тензора 3-го ранга, т. е.
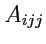
, и вычислим его значения в системе
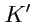
. Тогда
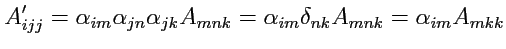 |
(278) |
и свертка
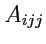
пребразуется как тензор ранга
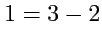
.