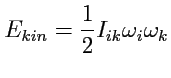В силу равноправия пространственных координатных систем, уравнения, выражающие физические законы, должны иметь одинаковые форму и соответственно решения в любой из этих систем. Это требование означает, что уравнения должны быть записаны в тензорной форме. Действительно, пусть в системе задано тензорное уравнение

Умножим (270) слева на и просуммируем по индексам . Тогда

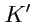
и, как видно, вид тензорных уравнений при переходе в систему не изменился. В качестве примера можно рассмотреть выражение для 2-го закона Ньютона:

Выражение для кинетической энергии вращающегося тела

также является примером ковариантного тензорного выражения.