![]() Тема 2. Элементы теории множеств и комбинаторика
Тема 2. Элементы теории множеств и комбинаторика
Множество относится к математическим объектам, для которых нет строгого
определения. Другим примером неопределяемого понятия служит точка в геометрии. Такие понятия
вводятся на интуитивном уровне, но зато на их основе даются строгие определения других
математических объектов.
Под множеством понимают объединение в одно целое объектов,
связанных между собой неким свойством. Термин "множество" в математике не всегда
обозначает большое количество предметов, оно может состоять из одного элемента
и вообще не содержать элементов, тогда его называют пустым и обозначают
Æ.
Если из элементов двух множеств можно составить пары таким образом,
чтобы каждому элементу первого множества соответствовал определенный элемент второго множества,
а каждому элементу второго множества соответствовал один и только один элемент первого множества,
то говорят, что между такими двумя множествами установлено взаимно однозначное
соответствие.
Чтобы установить взаимно однозначное соответствие, необязательно пересчитывать элементы множеств.
Например, мы знаем, что американские штаты находятся во взаимно однозначном соответствии с их
столицами, хотя можем оставаться в неведении относительно общего их числа. Мы могли бы утверждать:
«Столиц штатов ровно столько, сколько штатов».
Конечное множество состоит из конечного числа элементов,
например, множество страниц в книге, множество студентов в группе и т.д.
Бесконечное множество состоит из бесконечного числа элементов,
т.е. это множество, которое не является ни конечным, ни пустым. Например: множество действительных
чисел, множество точек плоскости, множество атомов во Вселенной и т.д.
Мощностью конечного множества называется количество его
элементов. Мощность множества A обозначается m (A).
Пример 1. Определите мощность какого из множеств
A = {1, 3, 5, 7, 9} или B = {2, 4, 6, 8} больше.
Решение. Понятие мощности конечных множеств позволяет
сравнивать их по количеству элементов. Так, если A = {1, 3, 5, 7, 9},
а B = {2, 4, 6, 8}, то m (A) = 5, а m (B) = 4
и потому m (A) > m (B).
Однако если мы имеем дело с бесконечными множествами, то пересчитать элементы множества уже не удастся. Но иногда можно, как говорят, установить взаимно однозначное соответствие между двумя бесконечными множествами.
Между двумя конечными множествами можно установить
взаимно однозначное соответствие тогда и только тогда, когда оба множества состоят из одного
и того же числа элементов.
В теории множеств аналогичные утверждения используются даже когда множества
содержат бесконечно много элементов. Если между двумя множествами можно установить взаимно
однозначное соответствие, то говорят, что они имеют одинаковое количество элементов
или равномощны. Если же при любом способе образования пар некоторые элементы из первого
множества остаются без пары, то говорят, что первое множество содержит больше элементов, чем второе,
или, что первое множество имеет большую мощность.
Счётное множество – множество, элементы которого можно пронумеровать.
Например, множества натуральных, чётных, нечётных чисел. Счётное множество может быть
конечным (множество книг в библиотеке) или бесконечным
(множество целых чисел).
Несчётное множество – множество, элементы которого невозможно
пронумеровать. Например, множество действительных чисел. Несчётное множество может быть только
бесконечным.
Множества обычно обозначаются большими буквами А,
В, С,…, а их элементы - малыми: а,
в, с…
Запись а Для задания множества следует:
![]() 1. Понятие о множестве
1. Понятие о множестве
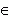 A означает,
что элемент а принадлежит множеству A,
то есть а является элементом множества A. В противном случае,
когда а не принадлежит множеству A, пишут а
A означает,
что элемент а принадлежит множеству A,
то есть а является элементом множества A. В противном случае,
когда а не принадлежит множеству A, пишут а
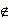 A.
A.
Таким образом, множество однозначно определяется его элементами и не зависит от порядка записи этих элементов.
Например, множество из трех элементов a, b, c допускает шесть видов записи:
{a, b, c} = {a, c, b} = {b, a c} = {b, c, a} = {c, a, b} = {c, b, a}.
Множество B называют подмножеством множества А, если любой элемент множества В является элементом множества А. Обозначается В Ì А (Рис. 1).
Пример. Пусть А, В,
С - подмножества множества N:
А={1, 2, 6, 18}; В={6, 1, 18};
С={2, 18, 6, 1}.
В этом случае А = С;
C Ì
A и A Ì
C, B Ì
A. Свойства включения множеств:
Геометрически множества обычно изображаются как
некоторые подмножества точек плоскости. В любой имеющей смысл задаче обычно
рассматриваются подмножества некоторого "наибольшего" множества U,
которое называют универсальным множеством. Универсальное множество - это самое
большее множество, содержащее в себе все множества, рассматриваемые в задаче.
На диаграммах Эйлера - Венна универсальное множество обозначают в виде
прямоугольника и буквы U. На рисунке 3 изображено универсальное множество U и два его подмножества - множества А
и В, B Ì
A (Рис. 3).
Картинки, представленные на рисунках 1-3 называются диаграммами
Эйлера-Венна.
|
|
| Рис. 3. Универсальное множество U и два его подмножества А и В |
Примеры.