Два множества A и B называются
равными, если они состоят из одних и тех же элементов, т. е. если каждый элемент
множества A принадлежит множеству B и, обратно, каждый элемент B
принадлежит A. Следовательно, два множества равны, если каждое из
них является подмножеством другого
(A = B Û (A
Ì B и В
ÌА)).
Множества не равны, если хотя бы в одном множестве существует хотя бы один элемент,
не принадлежащий другому множеству.
Любая математическая дисциплина, наряду с исходными, неопределяемыми, понятиями,
должна включать и "правила игры", способы работы с этими объектами. Например, числа в арифметике
можно складывать и умножать: говорят, что заданы операции сложения и умножения. Далее вводятся аналогичные
операции для множеств.
Объединением множеств А и В
называется множество С, состоящее из всех элементов,
принадлежащих хотя бы одному из данных множеств (т. е. либо
A, либо B, либо одновременно и A и B).
Объединение множеств обозначается символами "+" и
"U": C = A
U B.
Пример. Даны множества А = {-6, -3, 0, 3, 6}
и B = {0, 2, 4, 6, 8}. Тогда A
U B = {-6, -3, 0, 2, 3, 4, 6, 8}. Геометрически объединение
множеств изображено на рисунке 4.
Пример. Объединением множества рациональных чисел с множеством иррациональных
чисел является множество действительных чисел.
Пересечением множеств А и В
называется множество С, состоящее из элементов, принадлежащих одновременно и множеству
А, и множеству В. Если множества А и В
не имеют общих элементов, их пересечение равно пустому множеству Æ; в этом случае множества
А и В называются непересекающимися. Пересечение множеств
обозначается символами "∩" и "•" (знак умножения):
С = А ∩ В или С = АВ.
Пример. Даны множества А = {-6, -3, 0, 3, 6} и
B = {0, 2, 4, 6, 8}. Тогда A ∩ B = {0, 6}.
Геометрически пересечение множеств представлено на рисунке 5.
Пример. Пересечением множества целых чисел с множеством
положительных чисел является множество натуральных чисел.
Разностью множеств А и В
называется множество А\В, содержащее те элементы множества А, которые
не принадлежат множеству В.
В определении разности множеств А и В
не предполагается, что В является подмножеством множества A (Рис. 6).
Если же В подмножество A, то разность А\В называется
дополнением множества В до множества А (Рис. 7).
Для дополнения множества А до универсального множества U применяется
обозначение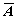 
(Рис. 8).
Пример. Нуль является дополнением множества натуральных чисел относительно множества
неотрицательных целых чисел.
Пример. Предположим, что множество U
состоит из всех букв русского алфавита, A – из всех согласных, а множество B
– из букв, встречающихся в слове «энциклопедия». Тогда
- объединение множеств A и B состоит из всех букв алфавита,
кроме а, ё, у, ъ, ь, ы, ю;
- пересечение множеств A и B – из букв д, к, л, н, п,
ц;
- дополнение множества А до универсального множества U
– из всех гласных.
Свойства операций
вверх
Тема 2. Элементы теории множеств и комбинаторика