Тема 2. Элементы теории множеств и комбинаторика

1. Понятие о множестве.
2. Операции над множествами.
3. Общие правила комбинаторики.
   Лабораторная работа № 2.   Операции над множествами. Общие правила комбинаторики.

3. Общие правила комбинаторики

Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств – правило суммы и правило произведения.

Правило суммы: пусть имеется n попарно непересекающихся множеств A1, A2, …, An , содержащих m1, m2, …, mn элементов соответственно. Число способов, которыми можно выбрать один элемент из всех этих множеств, равно m1 + m2 + … + mn.

Пример. Если на первой полке стоит X книг, а на второй Y, то выбрать книгу с первой или второй полки, можно X+Y способами.

Пример. Ученик должен выполнить практическую работу по математике. Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькими способами он может выбрать одну тему для практической работы?

Решение: По правилу суммы получаем 17+13=30 вариантов.

Кортеж - конечная последовательность (допускающая повторения) элементов какого-нибудь множества.

Правило произведения: пусть имеется n множеств A1, A2, …, An содержащих m1, m2, …, mn элементов соответственно. Число способов, которыми можно выбрать по одному элементу из каждого множества, т. е. построить кортеж (а1, а2, ..., аn), где аi Î А i1 (i = 1, 2, …, n), равно m1 · m2 · … · mn.

Пример. Если на первой полке стоит 5 книг, а на второй 10, то выбрать одну книгу с первой полки и одну со второй можно 5*10=50 способами.

Пример. Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневые переплеты. Сколькими способами он может это сделать?

Решение. Имеется 12 книг и 3 цвета, значит по правилу произведения возможно 12*3=36 вариантов переплета.

Выборки. Если из множества предметов выбирается некоторое подмножество, то его называют выборкой. Выборки бывают упорядоченные и неупорядоченные.

В упорядоченной выборке существенен порядок, в котором следуют ее элементы, другими словами, изменив порядок элементов, мы получим другую выборку.

Пример. Из цифр 1, 2, 3, 4, 5 можно составить следующие трехзначные числа 123, 431, 524, ...и т.д. Это упорядоченные трехэлементные выборки, так как 123 и 132 - разные числа.

Пример. Из 20 учащихся класса выбрать двух дежурных. Любая пара дежурных представляет собой неупорядоченную двухэлементную выборку, так как порядок их выбора не важен.

Размещения

Размещениями из n элементов по m элементов (m < n) называются комбинации, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком элементов.

Число размещений без повторений из n по m (n различных элементов) вычисляется по формуле:

(3.1)

Размещениями с повторениями из n элементов по m называются упорядоченные m-элементные выборки, в которых элементы могут повторяться.

Число размещений с повторениями вычисляется по формуле:

(3.2)

Пример. Возьмем буквы Б, А, Р. Какие размещения из этих букв, взятых по две, можно получить? Сколько таких наборов получиться, если: 1) буквы в наборе не повторяются; 2) буквы могут повторяться?

Решение.

  1. Получатся следующие наборы: БА, БР, АР, АБ, РБ, РА.

    2. По формуле (3.1) получаем: 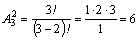наборов.

  2. Получатся наборы: ББ, БА, БР, АА, АБ, АР, РР, РБ, РА.

    3. По формуле (3.2) получаем: наборов.

Пример. Вдоль дороги стоят 6 светофоров. Сколько может быть различных комбинаций их сигналов, если каждый светофор имеет 3 состояния: "красный", "желтый", "зеленый"?

Решение. Выпишем несколько комбинаций: КККЖЗЗ, ЗЗЗЗЗЗ, КЖЗКЖЗ... Мы видим, что состав выборки меняется и порядок элементов существенен (ведь если, например, в выборке КЖЗКЖЗ поменять местами К и Ж, ситуация на дороге будет другой). Поэтому применяем формулу (3.2) и вычисляем число размещений с повторениями из 3 по 6, получаем комбинаций.

Перестановки

Перестановками из n элементов называются размещения из этих n элементов по n (Перестановки - частный случай размещений).

Число перестановок без повторений (n различных элементов) вычисляется по формуле:

(3.3)

Число перестановок c повторениями (k различных элементов, где элементы могут повторяться m1, m2, …, mk раз и m1 + m2 +… + mk = n, где n - общее количество элементов) вычисляется по формуле:

(3.4)

Пример. Возьмем буквы Б, А, Р. Какие перестановки из этих букв можно получить? Сколько таких наборов получится, если: 1) буквы в наборе не повторяются; 2) буква А повторяется два раза?

Решение.

  1. Получатся наборы: БАР, БРА, АРБ, АБР, РАБ, РБА.

    2. По формуле (3.3) получаем: наборов.

  2. Получатся наборы: БАРА, БРАА, БААР, ААРБ, ААБР, АБАР, АРАБ, АРБА, АБРА, РАБА, РААБ, РБАА.

    3. По формуле (3.4) получаем: наборов.

Пример. Сколько шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5 так, чтобы цифры в числе не повторялись?

Решение. Из данных шести цифр можно составить Р6 = 6! = 720 перестановок. Но числа, начинающиеся на нуль, не являются шестизначными. Такие числа отличаются друг от друга перестановкой пяти остальных цифр, значит, их будет Р5 = 120. Поэтому шестизначных чисел будет 720 - 120 = 600 чисел.

Пример. Сколькими способами можно расставить белые фигуры (2 ладьи, 2 коня, 2 слона, ферзь и король) на первой линии шахматной доски?

Решение. Первая линия шахматной доски представляет собой 8 клеток, на которых и надо расположить эти 8 фигур. Различные варианты расположения будут отличаться только порядком фигур, значит, это будут перестановки с повторениями Р8 (2,2,2).

По формуле (3.4) получаем: способов.

Сочетания

Сочетаниями из n элементов по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом (отличие сочетаний от размещений в том, что в сочетаниях не учитывается порядок элементов).

Число сочетаний без повторений (n различных элементов, взятых по m) вычисляется по формуле:

(3.5)

Число сочетаний c повторениями (n элементов, взятых по m, где элементы в наборе могут повторяться) вычисляется по формуле:

(3.6)

Пример. Возьмем буквы Б, А, Р. Какие сочетания из этих букв, взятых по две, можно получить? Сколько таких наборов получится, если: 1) буквы в наборе не повторяются; 2) можно брать по два одинаковые буквы.

Решение.

  1. Получатся наборы: БА (БА и АБ - один и тот же набор), АР и РБ

    2. По формуле (3.5) получаем: наборов.

  2. Получатся наборы: ББ, БА, БР, АА, АР, РР.

    3. По формуле (3.6) получаем: наборов.

Пример. Из 20 учащихся надо выбрать двух дежурных. Сколькими способами это можно сделать?

Решение. Надо выбрать двух человек из 20. Ясно, что от порядка выбора ничего не зависит, то есть Иванов-Петров или Петров-Иванов - это одна и та же пара дежурных. Следовательно, это будут сочетания из 20 по 2.

По формуле (3.5) получаем: способов.

Пример. В хлебном отделе имеются булки белого и черного хлеба. Сколькими способами можно купить 6 булок хлеба?

Решение. Обозначая булки белого и черного хлеба буквами Б и Ч, составим несколько выборок: ББББББ, ББЧЧББ, ЧЧЧЧЧБ, ... Состав меняется от выборки к выборке, порядок элементов несущественен, значит это - сочетания с повторениями из 2 по 6. По формуле (3.6) получаем способов.

Cделаем проверку и выпишем все варианты покупки: ББББББ, БББББЧ, ББББЧЧ, БББЧЧЧ, ББЧЧЧЧ, БЧЧЧЧЧ, ЧЧЧЧЧЧ. Их действительно 7.

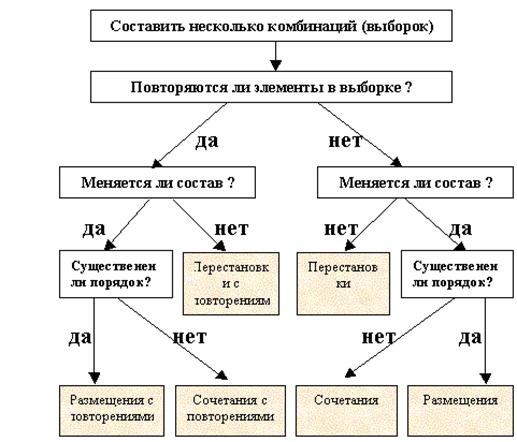
Схема определения вида комбинации:

Рис. 1.


вверх