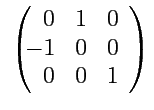Задачи для самостоятельной работы

1. Основные сведения из векторной алгебры

1.12. Задачи для самостоятельной работы

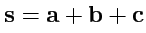
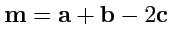
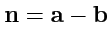
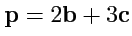
I. Разложить вектор ${\mathbf s}={\mathbf a}+{\mathbf b}+{\mathbf c}$ по трем некомпланарным векторам ${\mathbf m}={\mathbf a}+{\mathbf b}-2{\mathbf c}$ , ${\mathbf n}={\mathbf a}-{\mathbf b}$ и ${\mathbf p}=2{\mathbf b}+3{\mathbf c}$ . (Ответ)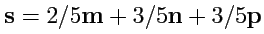

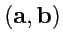
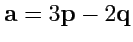
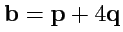
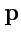
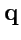
II. Вычислить скалярное произведение $({\mathbf a},{\mathbf b})$ , если ${\mathbf a}=3{\mathbf p}-2{\mathbf q}$ и ${\mathbf b}={\mathbf p}+4{\mathbf q}$ , где ${\mathbf p}$ и ${\mathbf q}$ - единичные, взаимно перпендикулярные векторы. (Ответ)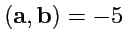

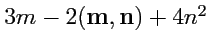
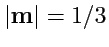
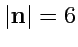
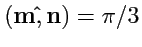
III. Найти числовое значение скаляра $3m-2({\mathbf m},{\mathbf n})+4n^2$ , если $\vert{\mathbf m}\vert=1/3$ , $\vert{\mathbf n}\vert=6$ и $(\hat{{\mathbf m},{\mathbf n}})=\pi/3$ . (Ответ)(143)

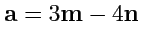
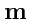
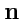
IV. Найти длину вектора ${\mathbf a}=3{\mathbf m}-4{\mathbf n}$ , если ${\mathbf m}$ и ${\mathbf n}$ - взаимноперпендикулярные, единичные векторы.

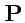
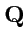
V. К одной точке приложены две силы ${\mathbf P}$ и ${\mathbf Q}$ , действующие под углом

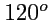
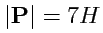
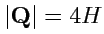
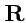
, причем $\vert{\mathbf P}\vert=7H$ , $\vert{\mathbf Q}\vert=4H$ . Найти величину равнодействующей силы ${\mathbf R}$ . (Ответ)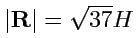

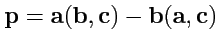
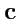
VI. Проверить, что векторы ${\mathbf p}={\mathbf a}({\mathbf b},{\mathbf c})-{\mathbf b}({\mathbf a},{\mathbf c})$ и ${\mathbf c}$ перпендикулярны друг другу.

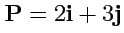
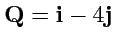
VII. Вычислить площадь параллелограмма, построенного на векторах ${\mathbf P}=2{\mathbf i}+3{\mathbf j}$ и ${\mathbf Q}={\mathbf i}-4{\mathbf j}$ . (Ответ)(11)

VIII. Доказать, что смешанное произведение векторов, из которых два коллинеарны, равно нулю.

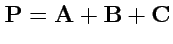
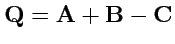
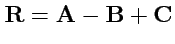
IX. Вычислить объем параллелепипеда, построенного на векторах ${\mathbf P}={\mathbf A}+{\mathbf B}+{\mathbf C}$ , ${\mathbf Q}={\mathbf A}+{\mathbf B}-{\mathbf C}$ , ${\mathbf R}={\mathbf A}-{\mathbf B}+{\mathbf C}$ . (Ответ)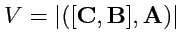

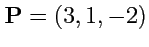
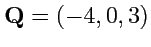
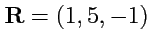
X. Вычислить объем параллелепипеда, построенного на векторах ${\mathbf P}=(3,1,-2)$ , ${\mathbf Q}=(-4,0,3)$ , ${\mathbf R}=(1,5,-1)$ . (Ответ)(V=6)

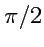
XI. Записать матрицу преобразования ортов системы координат XYZ к системе X'Y'Z', если она получается с помощью поворота системы координат XYZ вокруг оси Z на угол $\pi/2$ и проверить ее ортогональность. (Ответ)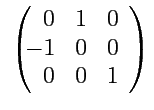

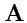
XII. Относительно системы координат XYZ вектор ${\mathbf A}$ имеет координаты

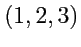
. Найти координаты ${\mathbf A}$ в системе X'Y'Z' (задача XI). (Ответ)(2, -1, 3)