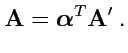5. Основы тензорного анализа

Физическое определение тензора 5.2. Общее определение тензора. Скаляры и векторы Тензоры 2-го ранга


Тензором ранга $ n$ называется совокупность $ 3^n$ величин $ T_{i_1,i_2,...,i_n}$, которые при переходе из одной системы координат в другую, преобразуются по закону
$\displaystyle T'_{i'_1,i'_2,...,i'_n} = \alpha_{i'_1,i_1} \alpha_{i'_2,i_2}...\alpha_{i'_n,i_n} T_{i_1,i_2,...,i_n}.$ (258)
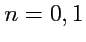
Из определения тензора ранга $ n$ следует, что скаляры и векторы являются частными случаями таких величин. Действительно рассмотрим случаи с $ n=0,1$, тогда скаляром или тензором ранга 0 называется набор из 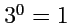$ 3^0=1$ величин 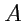$ A$, которые преобразуются по закону
$\displaystyle A' = A;$
 (259)
вектором или тензором ранга 1 называется совокупность $ 3^1=3$ величин $ A_i$, которые преобразуются по закону
$\displaystyle A'_i=\alpha_{ik}A_k\ $
 (260)
$\displaystyle A_i=\alpha_{ki}A'_k\ .$
 (261)
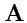
Если компоненты вектора $ {\mathbf A}$ расположить в виде столбца, то формулы преобразования можно записать в матричном виде
$\displaystyle {\mathbf A}' = {\boldsymbol \alpha}{\mathbf A} \phantom{...}$
 (262)
$\displaystyle {\mathbf A} = {\boldsymbol \alpha}^T{\mathbf A}'\ .$
 (263)

Векторный анализ в криволинейных координатах Литература
Физическое определение тензора   Содержание   Тензоры 2-го ранга