В случае евклидового пространства, в отличие от линейного аффинного, не все базисы равносильны по своим геометрическим свойствам. Среди них можно выделить наиболее простые - так называемые ортонормированные, которые в случае обычного пространства соответствуют базису прямоугольной декартовой системы координат.

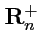
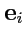
      Можно показать, что в -мерном комплексном пространстве и в вещественном собственно евклидовом пространстве всегда можно выбрать базисные векторы так, чтобы они удовлетворяли следующим условиям:

В этом случае, как видно, метрический тензор совпадает с единичным и на таких базисах теряется различие между ковариантными и контравариантными координатами и соответственно индексами, которые их нумеруют:

а все геометрические соотношения будут точно такими же, как и в обычном 3-х мерном пространстве, только лишь число координат будет равно .

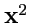
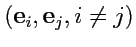
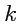
      Иная ситуация наблюдается в вещественных псевдоевклидовых пространствах, для которых, как уже отмечалось, может быть как положительным, так и отрицательным. 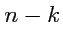В таких пространствах выбрать обычным образом ортонормированный базис нельзя, но можно выбрать ортогональных между собой векторов , таких, что часть из них (например, первые ) будут иметь квадрат длины, равный -1 (их называют мнимоединичными), а остальные соответственно - (). 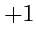Количество мнимоединичных векторов не зависит от выбора конкретного базиса, а определяется геометрической структурой псевдоевклидового пространства. 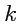Число таких мнимоединичных векторов называется индексом (сигнатурой) пространства. 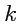может принимать одно из значений от 1 до и поэтому для заданного существует различных псевдоевклидовых пространств с различной сигнатурой.

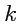
      В -мерном псевдоевклидовом пространстве индекса метрический тензор имеет структуру:

В силу структуры метрического тензора (355) различия между контравариантными и ковариантными координатами или векторами хотя и не исчезают, но становятся незначительными:

и тогда для скалярного произведения получаем: