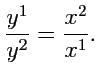5. Основы тензорного анализа
 5.20. Элементы геометрии 2-мерного псевдоевклидова пространства
5.20. Элементы геометрии 2-мерного псевдоевклидова пространства 
По своим аффинным свойствам псевдоевклидова плоскость (2-мерное линейное пространство)
ничем не отличается от обычной плоскости, однако по метрическим свойствам резко расходится
с ней (главное отличие состоит в наличии векторов с чисто мнимой длиной, которым
"нет места" на обычной плоскости). Ниже будут рассмотрены некоторые чертежи на плоскости,
которым нужно доверять лишь в той мере, в какой речь идет об аффинных свойствах, но отнюдь
не о метрических. Действительно, чертеж, сделанный на листе бумаги, отражает приблизительно
геометрию обычной плоскости. В данном случае плоскость не будет обычной и поэтому чертеж
будет верен лишь в тех пределах, в каких рассматриваются общие аффинные свойства. С метрическими
свойствами дело обстоит иначе. Например, ортогональные векторы или равные отрезки псевдоевклидовой
плоскости в условном изображении на чертеже, вообще говоря, ортогональными векторами и равными
отрезками выглядеть уже не будут. Не следует думать, что в этом есть что-то необычное. По
существу дело обстоит здесь совершенно так же, как и с картой земных полушарий, изображаемой
в виде плоских кругов на плоскости. Это изображение неизбежно содержит искажения, поскольку
геометрические свойства сферы и плоскости существенно различны, что не позволяет развернуть
сферу на плоскость подобно цилиндру, а искажения будут проявлятся в том, что расстояния,
равные на оригинале (сфере), будут различными на проекции (карте). Совершенно так же дело
обстоит в случае, когда оригиналом является псевдоевклидова плоскость, а ее условным
изображением - собственно евклидова плоскость чертежа.
Итак, рассмотрим 2-мерное псевдоевклидово пространство с сигнатурой (
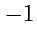
). Согласно определению,
существуют 2 линейно независимых вектора
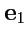
и
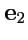
, и любой вектор
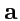
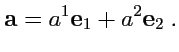 |
(358) |
В этом пространстве определено скалярное произведение
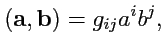 |
(359) |
причем базис можно выбрать ортонормированным:
![\begin{displaymath}\begin{array}{l} ({\mathbf e}_1,{\mathbf e}_2) = 0 \\ [1em] {\mathbf e}_1^2 = -1, \quad {\mathbf e}_2^2 = 1, \end{array}\end{displaymath}](img1347.png) |
(360) |
т. е. метрический тензор
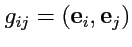
имеет вид следующей матрицы:
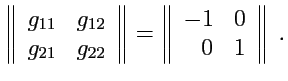 |
(361) |
Легко проверить, что обратная матрица координат контраваринатного метрического тензора
будет совпадать с (
361):
 |
(362) |
Связь между ковариантными и контравариантными координатами вектора

принимает
вид:
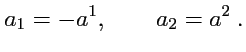 |
(363) |
Скалярное произведение (
359) в пространстве с метрическим тензором (
361) в
явном виде запишется как
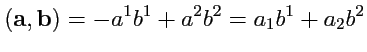 |
(364) |
и в частности
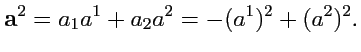 |
(365) |
Мы предпочтем использовать только контравариантные координаты
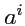
, так как они имеют аффинный
характер (коэффициенты разложения вектора
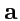
по базису
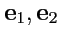
), и поэтому
их без ошибок можно измерять "по чертежу" т. е. как на обычной плоскости. Посмотрим, как будут
выглядеть на "чертеже" некоторые основные конструкции псевдоевклидовой плоскости (рис.
46).
Рис.46 Псевдоевклидова плоскость
Для простоты рассматриваемые векторы будем откладывать от точки О, учитывая, что по существу О -
любая точка псевдоевклидовой плоскости. Любой вектор
является линейной комбинацией
векторов
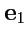
,
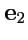
с коэффициентами (координатами)
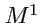
и
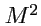
. В отличие от обычной
плоскости, на псевдоевклидовой существует не один изотропный вектор
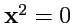
, совпадающий с
точкой О, а множество. Действительно, согласно (
365),ониимеютконтраваринтныекоординаты
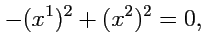 т. е. т. е.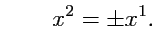 |
(366) |
Откладывая всевозможные изотропные векторы
от начала 0, видим, что их концы располагаются
на двух прямых (
366). С точки зрения собственно евклидовой геометрии листа бумаги, на котором
сделан чертеж, эти прямые являются биссектрисами координатных углов. Но с точки зрения псевдоевклидовой
геометрии такое их понимание не имеет никакого смысла.
Итак, через каждую точку О псевдоевклидовой плоскости проходят две изотропные кривые, которые испытывают,
очевидно, параллельный сдвиг при сдвиге точки О в любое новое положение. Неизотропные векторы, выходящие
из точки О, попадают в ту или иную пару вертикальных углов, образованных изотропными прямыми. При этом
под углом понимается область на плоскости, выделенная двумя прямыми, исходящими из общей точки, а отнюдь
не численная величина угла.
Рассмотрим сначала векторы, лежащие в одной паре вертикальных углов с ортом
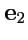
- вектор

.
Как видно из чертежа, для них

, а следовательно, согласно (
365)
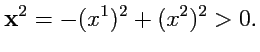 |
(367) |
Рис.47. Ортогональные векторы псевдоевкдидовой плоскости
Таким образом, в первой паре вертикальных углов углов расположены векторы вещественной длины (обычные
векторы с точки зрения евклидовой плоскости). В противоположность этому, векторы, лежащие во второй паре
вертикальных углов (заштрихованная область, вектор
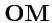
,
рис.46), характеризуются тем, что для них
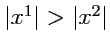
и, следовательно,
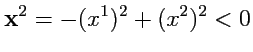 |
(368) |
и эти векторы обладают мнимой длиной (таких векторов в обычном евклидовом пространстве нет).
Рассмотрим, как выглядят в таком изображении ортогональные векторы псевдоевклидовой плоскости
(рис.
47). Пусть векторы
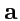
и
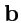
, имеющие контравариантные координаты
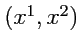
и
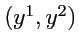
, ортогональны:
 |
(369) |
Отсюда
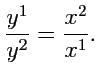 |
(370) |
Это означает, что в изображении, прямые, проходящие через эти векторы, имеют взаимнообратные
угловые коэффициенты и расположены симметрично относительно биссектрис координатного угла. Таким образом,
векторы, лежащие на двух прямых, симметричных относительно изотропной линии, ортогональны. Ортогональны
и сами прямые. Снова подчеркнем, что эта характеристика ортогональных прямых, данная с точки зрения
изображения, не имеет ни малейшего смысла с точки зрения оригинала, т. е. геометрии псевдоевклидовой
плоскости. Там эти прямые лишь ортогональны и ничего более.
Из полученного результата ясно, что вопреки обычному поведению ортогональных прямых на обычной плоскости,
вращение одной из них вызывает встречное вращение другой, причем, когда одна приходит в совпадение с
изотропной прямой, другая совпадает с ней же. Это и неудивительно, так как изотропная прямая, как направленная
по изотропному вектору, ортогональна к себе самой.
Теперь, чтобы составить представление о метрике псевдоевклидовой плоскости, будем откладывать от начала 0
Рис.48. "Окружность" псевдоевклидовой плоскости (действительный радиус)
отрезки данной постоянной длины
во всех направдениях, в которых это возможно сделать. Другими
словами, будем описывать окружность заданного радиуса
с центром в точке О. При этом радиус
окружности может быть как вещественным, так и чисто мнимым. Условие того, что вектор
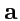
имеет
длину
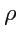
, имеет вид
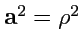
или
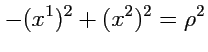 |
(371) |
(
371) и есть уравнение окружности на псевдоевклидовой плоскости. Пусть
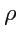
вещественно, тогда
уравнение (
371) определяет равнобочную гиперболу (рис.
48)
 |
(372) |
Причем, вторая, симметричная относительно координатной прямой
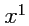
ветвь параболы так же будет принадлежать
"окружности", так как и на ней лежат концы векторов длины
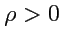
. Снова видно, что из-за несовпадения
геометрических свойств оригинала и его изображения "окружность" распадается на две разомкнутые ветви,
причем "радиусы", равные в оригинале, изображаются разными.
В случае
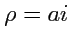
(
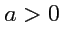
, радиус окружности чисто мнимый) "окружность" будет представляться уравнением
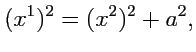 |
(373) |
Рис.49. "Окружность" псевдоевклидовой плоскости (мнимый радиус)
которое описывает две ветви гиперболы, симметричные относительно оси
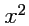
(рис.
49).
Наконец, в случае
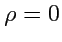
(точка на евклидовой плоскости), окружность нулевого радиуса сводится к
паре изотропных прямых.
![]() 5.20. Элементы геометрии 2-мерного псевдоевклидова пространства
5.20. Элементы геометрии 2-мерного псевдоевклидова пространства ![]()
 принимает
вид:
принимает
вид:
 , а следовательно, согласно (365)
, а следовательно, согласно (365)