2. Скалярные и векторные поля
 2.1 Функции скалярного и векторного аргумента
2.1 Функции скалярного и векторного аргумента 
В обычном анализе основным является понятие функции, т. е. закона, устанавливающего соответствие между элементами двух множеств: значений аргумента
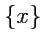
и значений функции
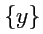
. Это
соответствие обычно обозначается следующим образом:
Обобщение функции одной переменной на числовую функцию

переменных состоит в том, чтобы
рассматривать в качестве аргумента не одно число, а упорядоченный набор

чисел
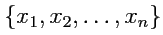
, в соответствие которому поставить значение функции
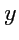
:
Вектор
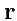
называется радиус-вектором и определяет точку пространства, в которой
задаются значения функций векторного аргумента.
Существует одно важное отличие перечисленных множеств векторов (1)-(3). В случае
(1) значения функции не зависят от пространственного положения начала вектора. Такие
векторы называются свободными и их можно привести к общему началу.
Для случая (3) этого сделать нельзя, поэтому такие векторы называются связанными.
В заключение следует отметить, что использование вектора как единой, самостоятельной величины,
позволяет использовать в анализе основное преимущество векторного исчисления - возможность
описания безотносительно к координатным системам, что оказывается очень важным для физических
приложений. Поэтому в дальнейшем все рассуждения будут строиться на основе именно этого
принципа.