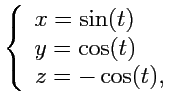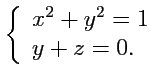2. Скалярные и векторные поля
 2.2 Вектор-функция скалярного аргумента. Производная
2.2 Вектор-функция скалярного аргумента. Производная 
Пусть множество значений вектор-функции скалярного аргумента

приведено к общему
началу в точке 0. Совместим с этой точкой начало декартовой системы координат. Тогда для
любого
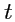
вектор

может быть разложен по ортам

:
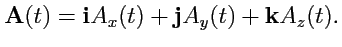 |
(46) |
Таким образом, задание вектор-функции скалярного аргумента означает задание трех
скалярных функций
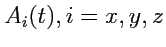
. В этом случае говорят, что вектор-функция задана
в декартовой системе координат. (Здесь и далее предполагается, что в сокращенной записи
с использованием индексных обозначений
,

,
и соответственно

,
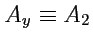
,

,
а также используется правило Эйнштейна суммирования по "немым" индексам).
При изменении значения аргумента
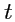
конец вектора

будет описывать в пространстве
кривую, которая называется
годографом вектора

. Например, в
механике, годографом радиус-вектора
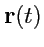
будет траектория движения. Согласно (
46)
уравнения годографа можно получить исключением
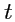
изуравнений
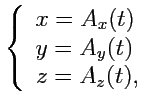 |
(47) |
что приводит в общем случае к системе уравнений вида:
![$\displaystyle \left\{\begin{array}{ll} \varphi_1(x,y,z) = 0\\ [0.5em] \varphi_2(x,y,z) = 0, \end{array} \right.$](img372.png) |
(48) |
которая определяет годограф, как линию пересечения двух поверхностей, уравнения которых
заданы функциями
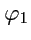
,
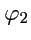
.
Пример 2-1. Определить годограф вектор-функции

.
Решение. Исключим параметр
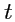
из системы уравнений:
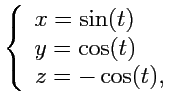 |
(49) |
например, как
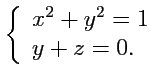 |
(50) |
Первое уравнение определяет круговой цилиндр с образующей, параллельной оси
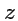
второе -
наклонную плоскость. Их пересечением будет эллипс, который и будет в этом случае годографом
функции

(рис.
11).
Рис.11. Годограф вектор-функции.
На вектор-функцию можно распространить такие понятия обычного анализа функций, как предел,
непрерывность, дифференцируемость. Так, вектор
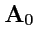
называется
пределом

при
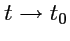
, если
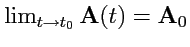
. Функция

называется
непрерывной при
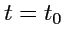
,если
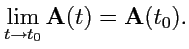 |
(51) |
Пусть для

существует близкое значение

. Тогда
производной вектор-функции поскалярному аргументу называется
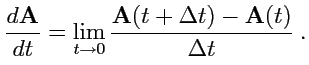 |
(52) |
Рис.12. К определению производной вектор-функции.
Согласно такому определению, производная вектор-функции также является вектор-функцией и поэтому
можно аналогично определить и высшие производные.
Рассмотрим геометрический смысл производной вектор-функции
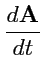
. Если взять два
значения

и

, то вектор
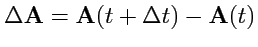
будет направлен по секущей
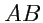
годографа. Тогда, из рис.
12 видно, что при
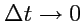
секущая будет стягиваться к касательной и, следовательно,
производная вектор-функции
направлена по касательной к годографу вектора

.
![$\displaystyle \left\{\begin{array}{ll} \varphi_1(x,y,z) = 0\\ [0.5em] \varphi_2(x,y,z) = 0, \end{array} \right.$](img372.png)