![]() Тема 4.
Основы теории вероятностей и математической статистики
Тема 4.
Основы теории вероятностей и математической статистики
Наблюдение явления, опыт, эксперимент, которые можно провести многократно,
в теории вероятностей принято называть испытанием. Результат, исход испытания
называется событием.
Пример 1. Сдача экзамена - это испытание; получение определенной
отметки - событие. Выстрел - это испытание; попадание в определенную область мишени - событие.
Бросание игрального кубика - это испытание; появление того или иного числа очков на брошенной
игральной кости - событие.
Виды случайных событий
События называются несовместными, если появление одного из
них исключает появления других событий в одном и том же испытании.
Пример 2:
Несколько событий образуют полную группу (пространство
исходов), если в результате испытания появиться хотя бы одно из них. Другими словами,
появление хотя бы одного из событий полной группы есть достоверное событие.
Пример 3. При сдаче
зачета возможны следующие исходы: «зачтено», «не зачтено», «не явился»; при подбрасывании монеты –
«орел», «решка».
Классическое определение вероятности
Пример 4. Пусть в урне содержится 6 одинаковых шаров, причем
2 из них - красные, 3 - синие и 1 - белый. Какова возможность вынуть наудачу из урны цветной шар?
Можно ли охарактеризовать эту возможность числом? Оказывается можно. Это число и называется
вероятностью события А (появления цветного шара). Таким образом, вероятность
есть число, характеризующее степень возможности появления события.
Каждый из возможных результатов испытания (в примере 4, испытание состоит в
извлечении шара из урны) называется элементарным исходом.
Те элементарные исходы, в которых интересующее нас событие наступает, называются
благоприятствующими этому событию. В примере 4 благоприятствуют событию
А (появление цветного шара) 5 исходов.
События называются равновозможными, если есть основания считать,
что не одно из них не является более возможным, чем другое.
Пример 5. Появление того или иного
числа очков на брошенном игральном кубике – равновозможные события.
Вероятностью P(A) события А называют отношение числа
благоприятствующих этому событию исходов к общему числу всех равновозможных
несовместных элементарных исходов, образующих полную группу. Вероятность P(A)
события А определяется по формуле
где m – число элементарных исходов, благоприятствующих
A; n – число всех возможных элементарных исходов испытания.
В примере 4 всего элементарных исходов 6; из них 5
благоприятствуют событию А. Следовательно, вероятность того что взятый шар окажется цветным,
равна P(A) = 5/6.
Пример 6. Определить вероятность выпадения нечётного числа очков на кости.
Решение. При бросании кости событие A –
«выпало нечётное число очков» можно записать как подмножество {1, 3, 5} пространства исходов
{1, 2, 3, 4, 5, 6} (рис. 1).
Рис. 1. Пространство исходов при бросании кости
Число всех равновозможных исходов n = 6, а число благоприятных
событию A – m = 3. Следовательно,
Пример 7. В урне находится 7 шаров: 2
белых, 4 черных и 1 красный. Вынимается один шар наугад. Какова вероятность того, что вынутый шар будет чёрным?
Решение. Занумеруем шары. Пусть, например, шары с номерами 1
и 2 – белые, с номерами 3, 4, 5 и 6 – чёрные, а
красному шару присвоим номер 7. Так как мы можем вынуть только
один из семи шаров, то общее число равновозможных исходов равно семи (n = 7).
Из них 4 исхода –
появление шаров с номерами 3, 4, 5 и 6 – приведут к тому, что вынутый
шар будет чёрным (m = 4).
Тем самым, вероятность события А, состоящего в появлении чёрного шара, равна
Вычислите вероятность того, что вынутый шар будет белым.
Пример 8. Вычислить вероятность выпадения в сумме 10 очков
при бросании пары костей.
Решение. Рассмотрим все равновозможные исходы в результате бросания
двух костей (их число равно 36 - рекомендуем записать в виде таблицы).
Выпадение в сумме 10 очков (событие А) возможно в трёх случаях –
4 очка на первой кости и 6 на второй, 5 очков на первой и 5 на второй, 6 очков на первой и 4 на второй.
Поэтому вероятность события А (выпадения в сумме 10 очков) равна
Свойство 1. Вероятность достоверного события
А равна единице:
Р(А) = 1.
Свойство 2. Вероятность невозможного события
А равна нулю:
Р(А) = 0.
Свойство 3. Вероятность случайного события есть положительное число,
заключенное между нулем и единицей: 0 £ P (A) £ 1.
Пример 9. Так как вероятность выпадения 13
очков при бросании пары костей – невозможное событие, его вероятность равна нулю.
Классическое определение вероятности предполагает, что число элементарных
исходов испытания конечно. На практике же часто встречаются испытания, число возможных исходов
которых бесконечно. Кроме этого, часто невозможно представить результат испытания в виде
совокупности элементарных событий. Еще труднее указать основания, позволяющие считать
элементарные события равновозможными. По этой причине, наряду с классическим определением
вероятности используют и другие определения, в частности статистическое определение.
Статистическое определение вероятности
Относительная частота наряду с вероятностью принадлежит к
основным понятиям теории вероятностей.
Относительной частотой события А называют отношение
числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний:
где m – число появлений события А, n – общее число
испытаний.
Классическая вероятность вычисляется до опыта, а относительная частота – после
опыта.
Длительные наблюдения показали, что если в одинаковых условиях производят опыты,
в каждом из которых число испытаний велико, то относительная частота обнаруживает свойство
устойчивости. Это свойство состоит в том, что в различных опытах относительная частота изменяется мало
(тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа.
Это постоянное число и есть вероятность появления события.
Таким образом, при достаточно большом количестве испытаний
в качестве статистической вероятности события принимают относительную
частоту или число, близкое к ней.
Пример 10. Естествоиспытатель К. Пирсон терпеливо подбрасывал
монету и после каждого бросания не ленился записывать полученный результат. Проделав эту операцию
24 000 раз, он обнаружил, что герб выпадал в 12 012 случаях. Вычисляя относительную частоту
выпадения герба, он получил
![]() 1. Определение вероятности
1. Определение вероятности
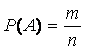 ,
,

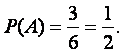
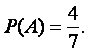
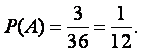
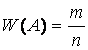 ,
,
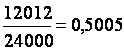 ,
что практически равно 1/2.
,
что практически равно 1/2.