Пример 2. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.

Решение. Появление цветного шара означает появление либо красного, либо синего шара.

Вероятность появления красного шара (событие А)

P (A) = 10/30 = 1/3.

Вероятность появления синего шара (событие В)

P (В) = 5/30 = 1/6.

События А и В несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима.

По формуле 2.1 искомая вероятность

P (A + B) = P(A) + P(B) = 1/3 + 1/6 = 1/2.

Теорема. Сумма вероятностей событий A₁, A₂, …, A_n , образующих полную группу, равна единице:

Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через А, то другое принято обозначать .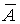

Пример 3. Если при бросании кости событие А состоит в выпадении 6, то противоположное событие – это невыпадение 6, т.е. выпадение 1, 2, 3, 4 или 5.

Пример 4: если А - число четное, то 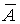- число нечетное; если А - зима, то 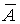- не зима (либо осень, либо лето, либо весна); если А - сдал экзамен, то 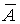- не сдал экзамен.

Пространство исходов иногда удобно изображать в виде прямоугольника, каждая точка которого соответствует элементарному событию. Это позволяет рассматривать произвольное событие А как подмножество пространства исходов (рис. 1).

Если исход испытания попадает в множество А, то говорят что в результате испытания событие А произошло, иначе что произошло противоположное событие (рис. 2).

Теорема. Сумма вероятностей противоположных событий равна единице:

P(А) + P() = 1.

(2.3)

Теоремы умножения вероятностей

Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий.

Пример 5: пусть А - из урны вытянули белый шар, B - из урны вытянули белый шар, тогда АВ - из урны вытянули два белых шара; если А - идет дождь, B - идет снег, то АB - дождь со снегом; А - число четное, B - число кратное 3, тогда АB - число кратное 6.

Событие В называют независимым от события А, если появление события А не изменяет вероятности события В.

Два события А и В называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события А и В называются зависимыми. Например, из одной колоды тянут карты, не возвращая их.

Условной вероятностью P_A(B) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.

Теорема умножения для зависимых событий

Теорема. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

Пример 6. В читальном зале имеется 6 учебников по информатике, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплете.

Решение. Рассмотрим следующие события:
А1- первый взятый учебник в переплете;
A2- второй взятый учебник в переплете.

Событие A = A₁ * A₂, состоит в том, что оба взятых учебника в переплете. События А₁ и А₂ являются зависимыми, так как вероятность наступления события А₂ зависит от наступления события А₁. Поэтому, для вычисления вероятности воспользуемся формулой (2.4).

Вероятность наступления события А₁ в соответствии с классическим определением вероятности:

P (А₁) = m / n = 3/6 = 0,5.

P _А1 (А₂) определяется как условная вероятность наступления события А₂ при условии, что событие А₁ уже наступило:

P _А1 (А₂) = 2/5 = 0,4.

Тогда искомая вероятность наступления события А:

P (А) = 0,5 * 0,4 = 0,2.

Теорема умножения для независимых событий

Теорема. Вероятность произведения двух независимых событий А и В равна произведению их вероятностей:

P(AB) = P(A)*P(B).

(2.5)

Теорема сложения вероятностей совместных событий

Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.

Пример 6. А - появление четырех очков при бросании игральной кости; В - появление четного числа очков. Событие А и В - совместны.

Теорема. Вероятность появления хотя бы одного из двух совместных событий А и В равна сумме вероятностей этих событий без вероятности их совместного появления:

P (A + B) = P (A) + P (B) - P (AB).

(2.6)

Пример 7. Два студента читают книгу. Первый студент дочитает книгу с вероятностью – 0,6; второй – 0,8. Найти вероятность того, что книга будет прочитана хотя бы одним из студентов.

Решение. Вероятность того, что книга будет прочитана каждым из студентов не зависит от результата отдельно взятого студента, поэтому события А (первый студент дочитал книгу) и B (второй студент дочитал книгу) независимы и совместны. Искомую вероятность находим по формуле 2.6.

Вероятность события АB (оба студента дочитали книгу):

P (AB) = P (A) * P (B) = 0,6 * 0,8 = 0,48.

Тогда

P (A + B) = 0,6 + 0,8 - 0,48 = 0,92.

Формула полной вероятности

Теорема. Вероятность события A, которое может наступить лишь при условии появления одного из несовместных событий B₁, B₂,…, B_n, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A:

(2.7)

Вероятность гипотез. Формулы Байеса

Теорема. Если существуют n попарно несовместных событий B₁, B₂,…, B_n, образующих полную группу, и известны условные вероятности события А, то можно найти вероятности того, что событие А произошло при условии появления некоторого события B_i по формуле:

.

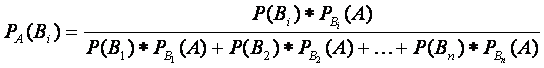(2.8)

Формулы Байеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.

вверх